Đối với sinh viên ngành đo đạc “bài toán cơ bản trong trắc địa” chắc hẳn sẽ không còn xa lạ nhưng không phải bạn nào cũng có thể nhớ rõ nó gồm những nội dung gì và cách để giải những bài toán đó. Bài viết sẽ tổng hợp các nội dung như sau: góc định hướng, bài toán thuận nghịch trong trắc địa và bài toán định độ cao trong trắc địa. Đây đều là những thông tin có ý nghĩa đối với sinh viên ngành trắc địa. Nếu bạn đang có nhu cầu tìm hiểu về ngành này hay là sinh viên trắc địa, đọc ngay những thông tin dưới đây để được hỗ trợ nhé!
Mục lục nội dung
Góc định hướng trong trắc địa
Bài toán về góc định hướng
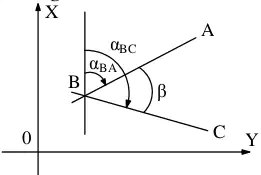
- Biết
và 
ta tính được góc 
- Biết và
ta tính được góc định hướng 
và 
ta tính được góc 
Áp dụng bài toán góc định hướng – 1 bài toán cơ bản trong trắc địa
Trong thực tế, thông thường ta không thể đo được góc định hướng mà chỉ đo được góc bằng 
, do đó để xác định góc định hướng của một đường thẳng phải dựa vào góc định hướng của một cạnh đã biết trước.
- Tính góc định hướng thực của góc trái
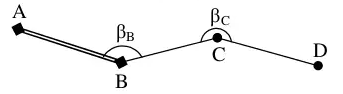
Theo chiều từ A, B, C, D thì các góc 
và 
nằm bên tay trái, khi đó:
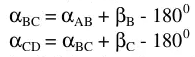
- Tính góc định hướng thực của góc phải
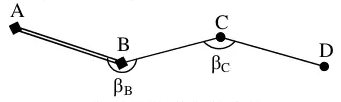
Theo chiều từ A, B, C, D thì các góc và nằm bên tay phải, khi đó:
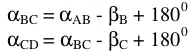
Bài toán thuận nghịch trong trắc địa
Dạng toán thuận nghịch vốn rất nổi bật, chúng có thể được bắt gặp trong mọi ngành nghề liên quan đến toán học. Trong bài viết này hãy cùng tìm hiểu về bài toán này cũng như những ảnh hưởng của nó trong ngành trắc địa như thế nào nhé.
Bài toán thuận trong trắc địa – bài toán cơ bản trong trắc địa
Bài toán thuận trong trắc địa là bài toán tính tọa độ vuông góc từ chiều dài và góc định hướng của cạnh.
Giả sử, biết tọa độ điểm A là XA và YB , Chiều dài cạnh giữa hai điểm A, B là SAB và góc định hướng của nó là 
.Tìm tọa độ điểm B
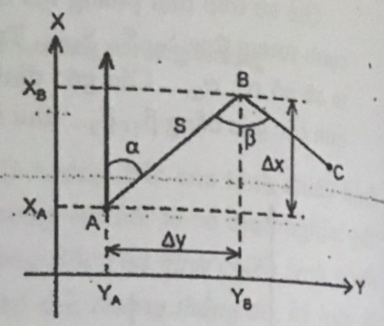
Từ hình trên ta có:
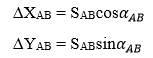
Do đó:
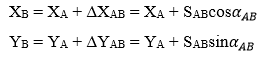
Ví dụ: Cho XA = 2325456,789 (m); YA = 18803234,725 (m); SAB = 1255,463 (m) và góc định hướng của cạnh SAB là 45020’32”2.
Ta tính được: XB = 2325456,789 + 1255,463cos45020’32”2 = 2326339,216 (m)
YB = 18803234,725 + 1255,463sin45020’32”2 = 18804127,759 (m)
Bài toán nghịch – 1 bài toán cơ bản trong trắc địa
Từ hình vẽ trên, nếu biết tọa độ của hai điểm A và B là XA, YA, XB, YB ta có thể tính được chiều dài cạnh SAB và góc định hướng của nó 
theo công thức:
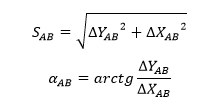
Nội dung của Bài toán thuận nghịch trong trắc địa được trình bày ở trên được sử dụng khi xử lý số liệu trong trắc địa.
Xem thêm:
Khảo sát hiện trạng rừng Bình Châu – Phước Bửu tại Xuyên Mộc phục vụ thiết kế
Giải Pháp Tính Toán Tín Chỉ Carbon Bằng Scan 3D Laser – Đảm Bảo Chính Xác & Hiệu Quả
Công ty dịch vụ đo đạc diện tích nhà chung cư cấp sổ hồng TPHCM
Công ty dịch vụ quét 3D Laser Scan công trình tại TPHCM
Bài toán định độ cao
Để chuyển độ cao tuyệt đối (H) của các điểm ta phải biết chênh cao (h) giữa các điểm đó. Có nhiều phương pháp xác định chênh cao nhưng thông dụng nhất là phương pháp đo cao hình học .
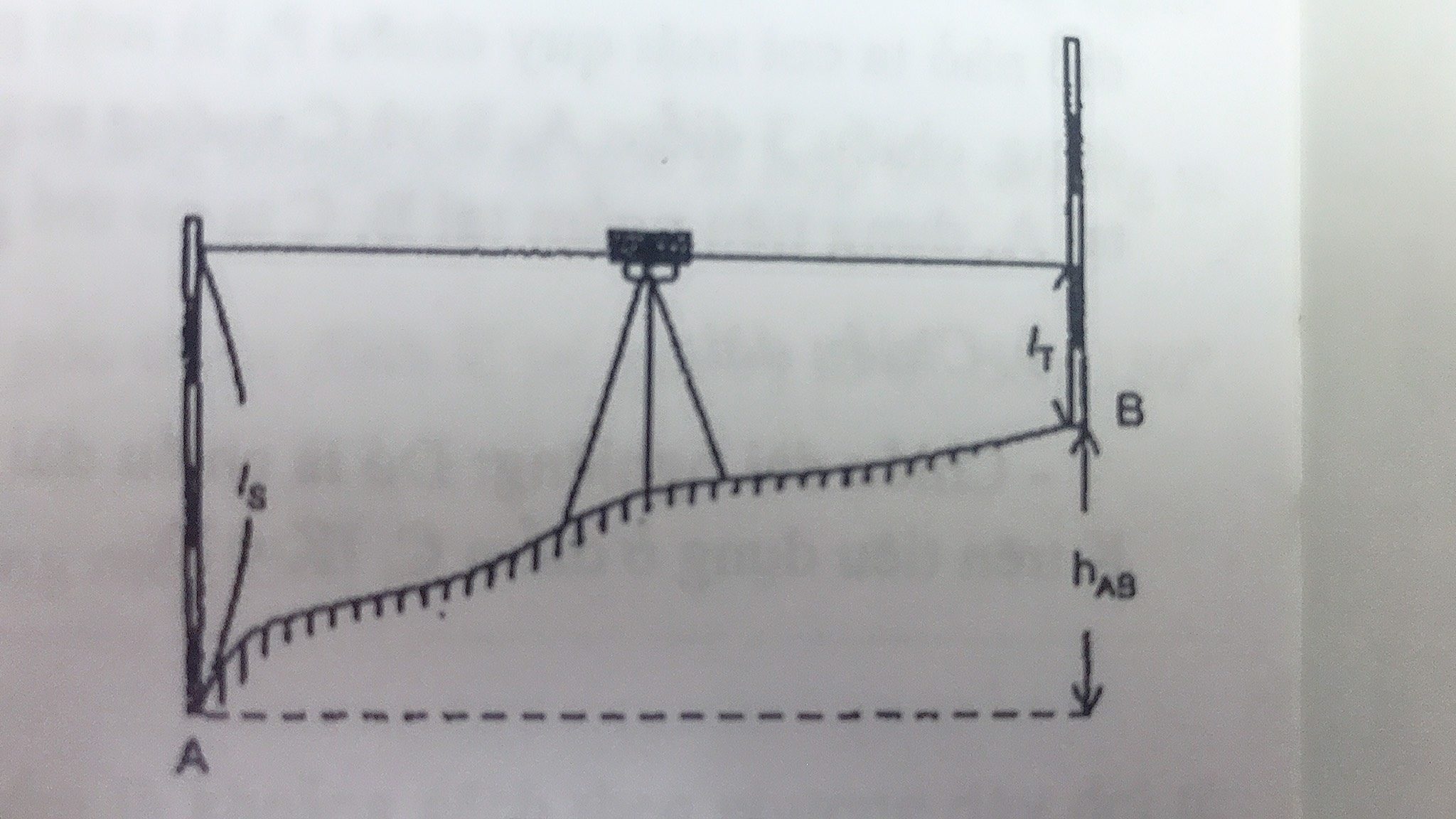
Trong phương pháp này để xác định hAB, tại điểm A và B đặt hai cái thước có khắc thành các vạch cm hoặc mm từ 0 đến 3 mét và gọi là mia.
Còn ở giữa đặt một thiết bị đo gọi là máy thủy chuẩn, máy này có khả năng đưa tia ngắm về vị trí nằm ngang (song song với mặt thủy chuẩn tại A) và đọc được chiều cao trên mia trước và mia sau là lT và ls. Từ hình trên ta có:
Trong đó: hAB là chênh cao giữa hai điểm A và B. Nếu ls = 1253mm, lT = 1042mm, ta có h = 211mm
Bằng phương pháp đo chênh cao giữa các điểm i, ta sẽ tính được độ cao Hi các điểm đó bằng cách tính chuyển độ cao tuyệt đối của điểm gốc (H0) đến các điểm đó.
Như vậy, chúng tôi đã giúp bạn tìm hiểu những thông tin cơ bản nhất về 3 dạng toàn cơ bản, thường gặp trong ngành trắc địa. Với những dạng toán này, bạn hoàn toàn có thể làm quen với cách giải toán trong ngành trắc địa cũng như ứng dụng chúng trong quá trình học tập, làm bài tập khi học trắc địa.
CÔNG TY TNHH HỢP NHẤT BÁCH VIỆT
Đo đạc địa chính – Khảo sát địa hình – Tính toán Carbon
Trụ sở chính: 369 Lò Lu, P. Trường Thạnh, Tp. Thủ Đức , TPHCM
Chi Nhánh Sông Tiền: Tổ 5, Ấp Thống Nhất, Xã Bình Phú, huyện Tân Hồng, tỉnh Đồng Tháp.
Địa điểm kinh doanh: 31/13 đường 160, phường Tăng Nhơn Phú A, thành phố Thủ Đức, thành phố Hồ Chí Minh.
Hotline: 0903692185 hoặc 0907621115
Email: viet@bachvietunited.com
