Chương trình học phổ thông đã giới thiệu đến các bạn về hệ tọa độ Oxyz và rất nhiều bài tập liên quan. Không chỉ trong toán học, hệ trục này cũng được ứng dụng rất rộng rãi trong đời sống, là nền tảng cho nhiều nghiên cứu kỹ thuật. Nếu như bạn đang muốn ôn luyện lại các kiến thức về hệ tọa độ không gian này cùng với những ứng dụng liên quan, hãy tham khảo nội dung được Đo Vẽ Nhanh chia sẻ sau đây.
Mục lục nội dung
Hệ tọa độ Oxyz là gì?
Theo như chương trình học phổ thông, có những bài toán hình học phẳng đã được dạy trong chương trình lớp 10. Hệ tọa độ không gian lớp 12 cũng là dạng toán thú vị, hữu ích. Việc đưa khái niệm này và các bài tập liên quan không chỉ giúp học sinh có thêm nhiều kiến thức bổ ích, rèn luyện tư duy không gian mà còn là nền tảng cho những chuyên môn sau này.
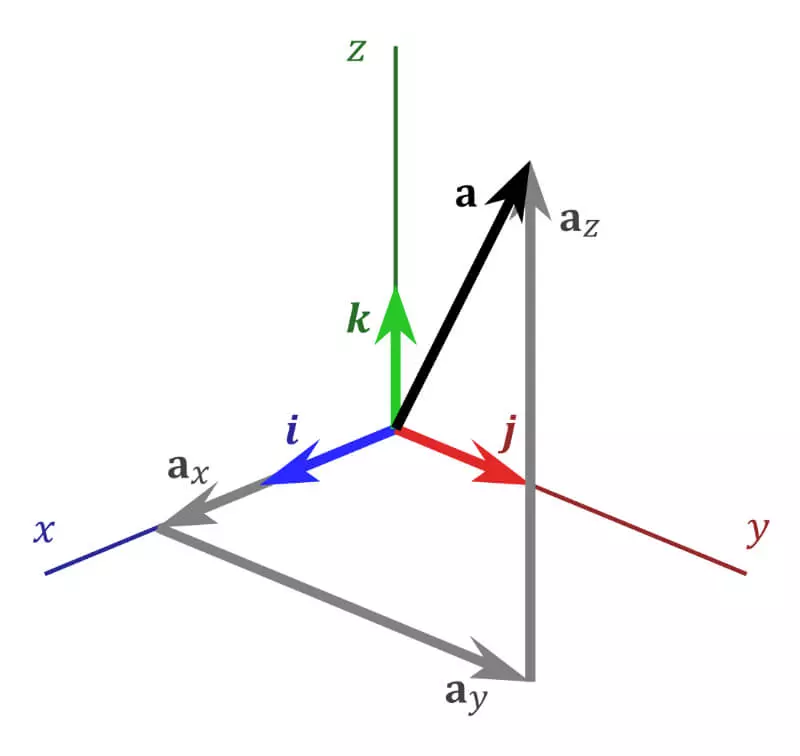
Theo đó, hệ tọa độ Oxyz là hệ tọa độ không gian trong đó, các đường thẳng là 3 trục Ox, Oy, Oz trong hệ từng đôi một vuông góc. Hệ trục này thể hiện không gian 3 chiều, có thể bắt gặp ở bất cứ đâu trong cuộc sống, chẳng hạn như góc ngôi nhà, vật thể hình hộp…Hình ảnh về hệ trục không gian tọa độ được thể hiện trong hình dưới đây:
Thuật ngữ và các ký hiệu hệ tọa độ không gian
Hệ trục tọa độ không gian, hay hệ tọa độ trong không gian Oxyz được ký hiệu trong toán học cụ thể như sau:
Các trục, vectơ và mặt phẳng đi qua hệ tọa độ Oxyz
- O(0;0;0) là gốc tọa độ .
- Các trục tọa độ lần lượt là Ox đóng vai trò trục hoành, Oy là trục tung, Oz là trục cao.
- i⃗ ,j⃗ ,k⃗ lần lượt là các vecto được gắn trên các trục Ox, Oy, Oz và chúng cũng đôi một vuông góc với nhau.
- Trong đó tọa độ các vecto này như sau: i⃗ =(1;0;0),j⃗ =(0;1;0),k⃗ =(0;0;1). Lưu ý rằng i⃗ 2=j⃗ 2=k⃗ 2=1.
- Công thức i⃗ .j⃗ =j⃗ .k⃗ =k⃗ .i⃗ =0
- Các mặt phẳng đi qua 2 trong 3 trục tọa độ lần lượt là các mặt phẳng tọa độ ( Oxy ), (Oyz), (Oxz), và đôi một vuông góc với nhau.
Tọa độ điểm và vecto trong hệ trục không gian
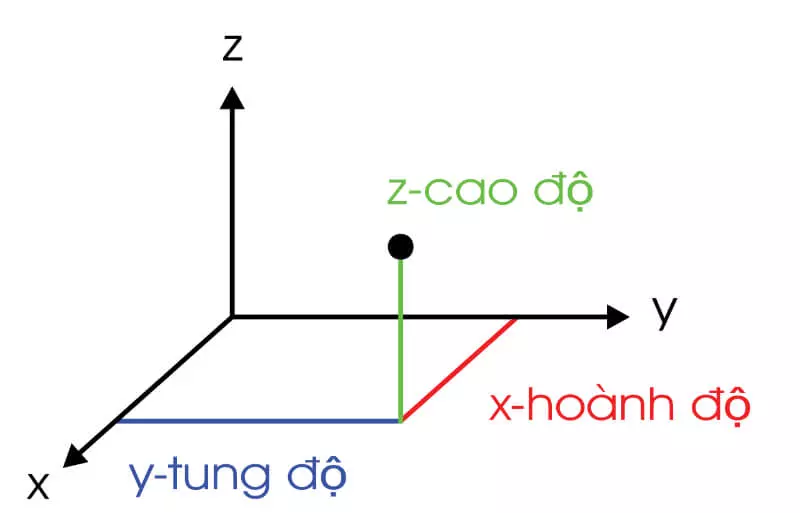
Giả sử có một điểm M trong hệ tọa độ Oxyz, ta có đoạn thẳng OM thỏa mãn công thức OM =xi⃗ +yj⃗ +zk⃗, Như vậy, điểm M có tọa độ M(x;y;z). Trong đó:
- x gọi là hoành độ thuộc trục hoành,
- y gọi là tung độ thuộc trục tung.
- z gọi là cao độ của điểm M.
Tọa độ của vecto thuộc hệ trục tọa độ không gian này là a⃗ =a1i⃗ +a2j⃗ +a3k⃗ , như vậy vecto a⃗ có tọa độ a⃗ =(a1;a2;a3).
Một số tính chất của hệ tọa độ không gian
Gỉa sử cho vecto a⃗ =(x1;y1;z1), b⃗=(x2;y2;z2) và một số k bất kỳ nào đó, ta có các tính chất cụ thể như sau:
- Tổng của hai vecto trả về kết quả là một vecto: a⃗ +b⃗ =(x1+x2;y1+y2;z1+z2).
- Hiệu của hai vecto trả về kết quả là một vecto: a⃗ −b⃗ =(x1−x2;y1−y2;z1−z2).
- Tích của hai vecto với một số thực K là một vecto: k.a⃗ =(kx1;ky1;kz1)
- Độ dài của vecto là |a⃗ |= √(x1²+y1²+z1²).
- Tọa độ của 0⃗ =(0;0;0).
- Tích vô hướng của hai vectơ như sau: a⃗ ⊥b⃗ ⇔a⃗. b⃗ =0.
Các công thức trong hệ tọa độ Oxyz
Trong không gian của hệ tọa độ Oxyz, cho hai điểm A và B có tọa độ A(xa;ya;za),B(xb;yb;zb), ta có:
- Tọa độ vecto AB→là: AB→=(xB−xA;yB−yA;zB−zA).
- Độ dài đoạn thẳng AB hay khoảng cách giữa hai điểm A và B được tính là độ dài của AB như sau: ∣AB→∣= √[(xB−xA)²+(yB−yA)²+(zB−zA)²].
- Tọa độ trung điểm I thuộc đoạn thẳng AB được tính theo công thức:
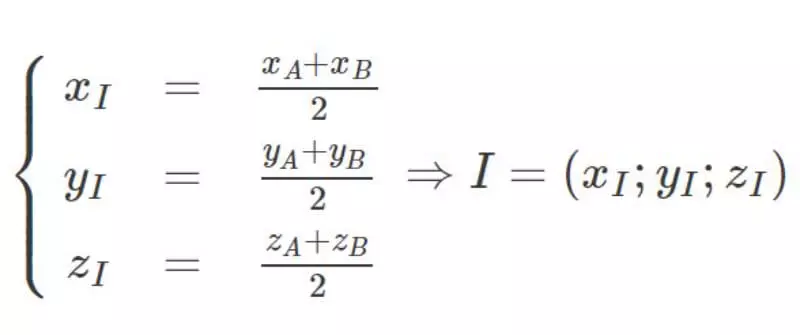
- Giả sử △ABC với A(xA;yA;zA),B(xB;yB;zB), C(xC;yC;zC), ta có tọa độ trọng tâm của tam giác này như sau:
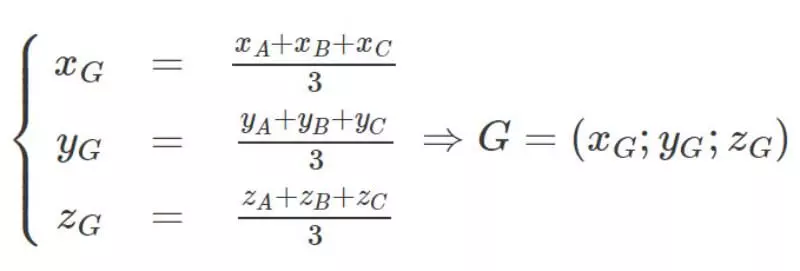
- Tích vô hướng của hai vectơ: a⃗ .b⃗ =x1x2+y1y2+z1z2.
Xem thêm:
Hệ trục tọa độ Oxy và những điều cần biết
Nghiên cứu: Gốc tọa độ và ứng dụng thực tiễn của nó
Ứng dụng của hệ tọa độ Oxyz vào đời sống
Hệ trục tọa độ Oxyz không chỉ là giảng dạy thông thường trong các chương trình học phổ thông. Ở những bậc học cao hơn, sẽ có những bài giảng, đào tạo chuyên sâu hơn về ứng dụng của nó trong đời sống, đặc biệt là trong đo đạc địa chính và xây dựng công trình. Mục đích lớn hơn là trong vũ trụ để tính khoảng cách giữa các hành tinh, xác định tọa độ điểm trên Trái đất…

Qua những thông tin trên đây, bạn đã có thêm những kiến thức bổ ích của hệ tọa độ Oxyz. Từ đó, có thêm những kiến thức để ứng dụng trong làm bài tập cũng như đời sống. Đừng quên đến với Đo Vẽ Nhanh nếu như có nhu cầu về đo đạc địa chính, khảo sát địa hình và tư vấn pháp lý nhé.
CÔNG TY TNHH HỢP NHẤT BÁCH VIỆT
Đo đạc địa chính – Khảo sát địa hình – Tính toán Carbon
Trụ sở chính: 369 Lò Lu, P. Trường Thạnh, Tp. Thủ Đức , TPHCM
Chi Nhánh Sông Tiền: Tổ 5, Ấp Thống Nhất, Xã Bình Phú, huyện Tân Hồng, tỉnh Đồng Tháp.
Địa điểm kinh doanh: 31/13 đường 160, phường Tăng Nhơn Phú A, thành phố Thủ Đức, thành phố Hồ Chí Minh.
Hotline: 0903692185 hoặc 0907621115
Email: viet@bachvietunited.com
